Goldener Schnitt und Fibonacci Zahlenfolge



Video als Einführung - Natur und Zahlen

Goldener Schnitt:

Der goldene Schnitt (auch stetige Teilung genannt) ist die Bezeichnung für die Teilung einer Strecke
durch einen auf ihr liegenden Punkt, so dass sich die ganze Strecke zum größeren Abschnitt
verhält wie der größere Abschnitt zum kleineren Abschnitt.

Teilung im goldenen Schnitt

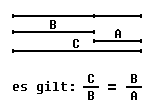
Für das Verhältnis B/A = C/B = phi ergibt sich die Zahl phi = 1,61803398874989484820458...
Für das Verhältnis A/B = B/C = phi ergibt sich die Zahl rho = 0,61803398874989484820458...
Die irrationalen Zahlen phi und rho werden als goldene Zahlen bezeichnet und können wie folgt berechnet werden.

Mit Quadratwurzel:

phi = (Wurzel(5)+1)/2
rho = (Wurzel(5)–1)/2

Mit Kettenbruch:

phi = 1 + 1/(1 + 1/(1 + 1/(1 + 1/(1 + 1/(1 + 1/...)))))...

Mit Winkelfunktionen:

phi = 1/(2 cos 72) = 1/(2 sin 18) = 2 sin 54 = 2 cos 36

Außerdem sind:

phi und –rho die Lösungen der quadratischen Gleichung x² – x – 1 = 0
–phi und rho die Lösungen der quadratischen Gleichung x² + x – 1 = 0

Besonderheiten dieser Zahlen:

phi x rho = 1
phi – rho = 1
phi + rho = Wurzel(5)
phi² = 1 + phi
rho² = 1 – rho
1 + phi = phi²
phi + phi²  = phi³
phi² + phi³ = phi^4

Die Regel des goldenen Schnittes wurde vielfach in der Kunst und der Architektur angewendet.
Dieses Zahlenverhältnis ist ein Grundprinzip in Natur und Schöpfung.

Man findet diese Proportionen annähernd, aber nie ganz perfekt in allen lebenden Strukturen.
Die Bezeichnungen Goldener Schnitt und stetige Teilung sind noch relativ jung. Sie wurden erst im 19. Jahrhundert geprägt.
Zum ersten Mal wird der Sachverhalt des Goldenen Schnitts von Euklid um 300 v. Chr. schriftlich festgehalten.
Allerdings wird davon ausgegangen, dass die stetige Teilung und insbesondere die exakte Konstruktion der Fünfeckteilung
bereits früher bei den Ägyptern oder bei den Pythagoräern mit deren Erkennungssymbol, dem Pentagramm, bekannt war.


Konstruktion vom Goldenen Schnitt:

 

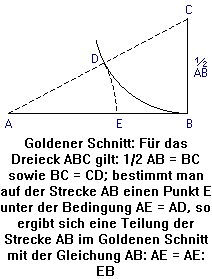
Anwendung des Goldenen Schnitts bei der Konstruktion eines regelmäßigen Fünfecks:

Es wird lediglich ein Lineal (auch ohne Maßeinteilung) und einen Zirkel benötigt. Zu Beginn hat man die Seite AC.
Wie oben gezeigt, werden nach dem Goldenen Schnitt zunächst die Punkte G und G` konstruiert. Dann werden, wie
in der Skizze abgebildet die beiden Kreise um die Punkte A und C und die Mittelsenkrechte zu AC konstruiert.
Der Punkt B ist der eine Schnittpunkt der beiden Kreise. Nun zeichnet man eine Gerade durch BG und eine
durch BG`. Diese Geraden schneiden die Kreise in den Punkten D und E. Das regelmäßige Fünfeck ergibt sich
aus den Punkten A,B,C,D,E. Die Konstruktion beruht darauf, dass sich die Diagonalen gegenseitig im Verhältnis
des Goldenen Schnitts teilen (z.B. AC mit BD im Punkt G).



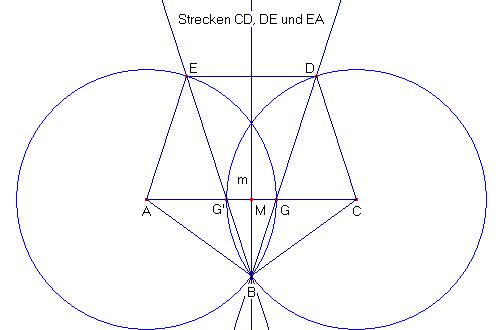
Noch eine alternative Möglichkeit für die Praxis:

In einen Papierstreifen, der überall gleich breit ist (z.B. 2cm breit und 20 cm lang) macht man einen
Knoten, drückt diesen vorsichtig platt und erhält ebenfalls ein regelmäßiges Fünfeck.


Zahlenfolge:

Eine Funktion mit einem bestimmten Definitionsbereich oder einer Teilmenge davon wird als Zahlenfolge bezeichnet.
Die Funktionswerte heißen Glieder der Zahlenfolge und werden nach festgelgeten Regeln bestimmt.

Üblicherweise bezeichnet man eine Zahlenfolge folgendermaßen:

(a_n): a₁ , a₂ , a_{3 ,} a₄ , ...
n = 1, 2, 3, ...

Beispiel: a_n = n*2 + 3 => 5, 7, 9, 11, ...


Fibonacci Zahlenfolge:

Bei der Fibonacci-Folge erhält man ein Glied durch Addition der zwei vorhergehenden Glieder.

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, ...

Regeln:  n = 0, 1, 2, 3, ...  /  a₀ = 0  /  a₁ = 1  /  a_n+2 = a_n + a_n+1

a₀ = 0
a₁ = 1
a₂ = 0 + 1 = 1
a₃ = 1 + 1 = 2
a₄ = 1 + 2 = 3
a₅ = 2 + 3 = 5
a₆ = 3 + 5 = 8
usw.

Die 0 am Anfang der Folge wird teilweise auch weggelassen. Sie steht symbolisch für
  den Kreis, den Nullpunkt, den Beginn, den Durchgang oder das DimensionsTor
in die Wirklichkeit der lebendigen Schöpfungen.

Die Fibonacci Zahlenfolge grafisch dargestellt:

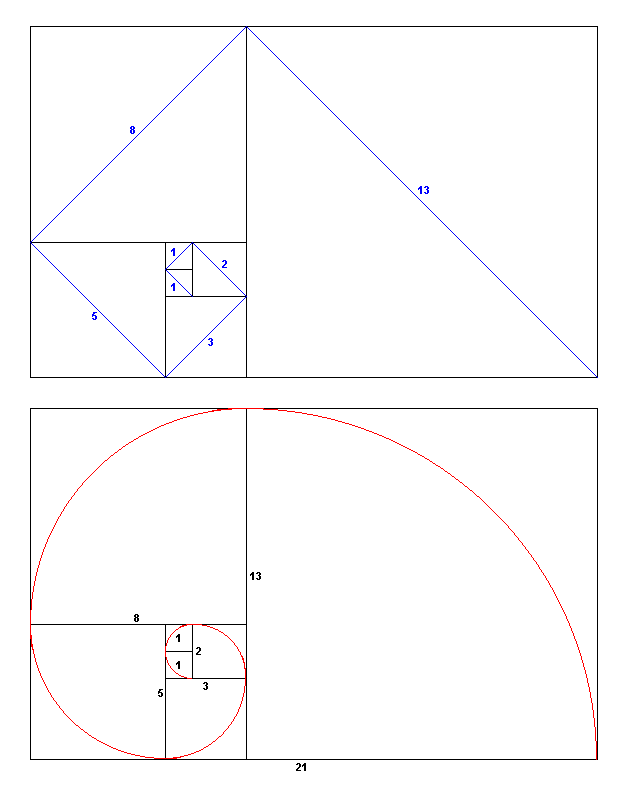
Die Arabischen Zahlen:

Die Zahlen 6 und 9 unserer arabischer Zahlen ähneln in ihrem Aussehen einer Fibonacci-Spirale, wie sie
oben dargestellt ist. Mir ist nicht bekannt, warum man die arabischen Zahlensymbole so sind, wie wir sie
kennen. Es ist jedoch ist zu vermuten, dass sich der Erschaffende etwas dabei gedacht hat. Die Verwendung
der Zahl 0 war Anfangs nicht üblich, da sie erst später aus Indien hinzukam. Schreibt man die Zahlen 1 bis 9
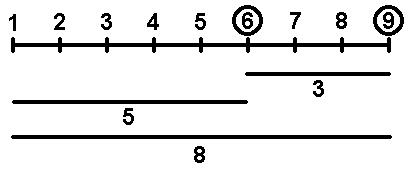
nacheinander in gleichen Abständen auf und nimmt die Zahlen 1, 6 und 9 als markante Punkte, so liegen:
3 Einheiten zwischen den Zahlen 6 und 9,
5 Einheiten zwischen den Zahlen 1 und 6,
8 Einheiten zwischen den Zahlen 1 und 9.

Die 3, 5 und 8 sind alles Zahlen aus der Fibonacci Zahlenfolge, die wiederum ein Ausschnitt der
Fibonacci-Spirale bilden und im Aussehen den Zahlen 6 und 9 ähneln. Das ist eine überaschende
Spielerei. Hat der Erschaffende hier einen Hinweis auf den goldenen Schnitt verewigt?


weitere Informationen über ähnlichen Themen:

Video - Hat Schönheit Regeln, der goldene Schnitt
Bücher über Heilige Geometrie: Drunvalo Melchizedek - Die Blume des Lebens (Band 1 und 2)
Artikel - Heilige Geometrie und die Blume des Lebens
Infos von einem der Konstrukteure des Giseh Plateaus: http://www.hores.org --> Veröffentlichungen
http://www.hores.org/artikel/mathe/mathe.html
http://www.mathematische-basteleien.de/goldenerschnitt.htm

<<< StartSeite <<<

Impressum

erstellt am: 02.05.2010